Co je vlastně Pravda? - 3. část

Matematika je docela zvláštní. Téměř nikdo ji nemá rád, ve škole se ji lidé učí spíš násilím a už vůbec v ní nevidí něco hlubšího nebo nedej bože i něco krásného. Nepopírám, matematika je rozhodně těžká záležitost a aby ji člověk rozuměl dost dobře, musí ji obětovat tisíce hodin studia. No a samozřejmě, většina lidí si ke studiu raději zvolí něco naprosto jiného.

Problém matematiky je ten, že se dost často ve školách vyučuje špatně a málokterý učitel své studenty inspiruje. A to proto, že přeložit matematiku do srozumitelných slov nebo vytvořit vhodné analogie je dost problematické. Ale věřte, že jakoukoliv rovnici lze skutečně do těch slov přeložit! Jen je to prostě těžké a vyžaduje to komplikovanou terminologii. Navíc, moderní matematika je dnes už někde úplně jinde, než byla před sto lety. Především v ni nejde ani tak o samotná čísla. Jenomže tohle je problém u každého předmětu - furt se na základních a středních školách učí stejná fyzika, stejná chemie, stejná teorie evoluce a stejná historie. Ale věci se mění hodně rychle a učebnice se nestíhají přepisovat. Nebo alespoň aktualizovat či zpřesňovat. Vážně ještě dnes někdo věří, že sumerská civilizace byla ta první?

Galileo Galilei kdysi řekl: "Velkou knihu přírody mohou číst jen ti, kteří znají jazyk, jímž byla napsána. A tím jazykem je matematika."
Jiný, ne úplně přesně známý zdroj taky řekl něco zajímavého: "Matematika se ve vaši říši učí takovým způsobem, že se naučí jen několik vybraných. A matematika je jazykem celé tvorby."

Dva zajímavé výroky, které celkem odpovídají skutečnosti. Pokud bychom chtěli nějakému mimozemšťanovi vysvětlit, co o tomhle světě opravdu víme, nejlépe bychom to popsali matematickými větami. Proč? Protože rovnice dosahují nejvyšší možné přesnosti odvozené naším aktuálním rozumem. Jde o skutečnosti, které jsou zbaveny subjektivity, emocí a vágních pojmů a které jsou založeny čistě na principu pravdy/nepravdy z precizně stanovených logických kroků. Jednoduše vše, co lze popsat matematikou, se nejvíce blíží pravdě, protože se jedná o neprůstřelné důkazy, které naše mysl dokáže uchopit. Matematika je vlastně disciplína, která je v tomhle světě to "nejpravdivější", co zatím máme. Zatím. No a taky je již na první pohled patrné, že o kalkul se zajímá jen mizivé procento lidí. Proč, to není zcela jasné.

Většina lidí tady ale namítne: "A naše oči? Nebo uši? To, co vidíme a slyšíme nebo i cítíme, není skutečné a pravdivé?"
No, skutečné to nějak jistě je. Vnímají to přece naše smysly. Ale jestli to je i pravdivé, to budeme muset někdy v budoucnu teprve zjistit. Málokdo si totiž uvědomuje, že mezi skutečností (realitou) a pravdou je určitý rozdíl. Pravda je monistická, realita ne. Vysvětlíme si to na jednoduchém příkladu s barvami.

Je známé, že lidé vnímají barvy docela individuálně. Když někomu ukážete třeba nějaký odstín zelené, jednomu se ten odstín bude zdát jako trávově zelený, druhému možná spíš jako smaragdový a třetímu zase jako jehličí borovice. Vizuální vjem je tedy hodně subjektivní. U pokusů s barvami bylo taky zjištěno, že lidé mohou vnímat stejné vlnové délky světla v různých odstínech, ale taky to mohou vnímat i obráceně - různé vlnové délky vidí pod stejným odstínem.
Takže, kdo má vlastně pravdu? Jaká konkrétní barva je opravdu viděna? Dalo by se říct, že každý vnímá nějakou "vlastní" barevnou skutečnost (realitu), no větší pravdivostní hodnotu má v tomto případě samotné světlo s konkrétní vlnovou délkou. Subjektivní vnímání barev jednotné prostě není. Pojďme se tedy nejdříve podívat na to, co nám vlastně sdělují naše smysly.


Smysly

Zrak, sluch, chuť, čich, dotek a termoreceptory nám pomáhají vnímat naše okolí. Všemožné informace zachycené zvenčí se nervovou soustavou přenášejí do mozku, který následně dané vjemy zpracuje a interpretuje a naše osoba potom tenhle interpretovaný vjem nějak vyhodnocuje - líbí se nám to, bolí nás to, je nám horko, vidíme něco krásného, slyšíme nepříjemný zvuk a tak dále. Máme tedy nějaký input, processing a output a naše já v tom hledá nějaký význam. Smysly jsou tedy něco jako "brána", která propouští do našeho nitra okolní svět. Celý vjem představuje velmi komplexní souhru, protože hodně záleží na každém stupni tohoto procesu - příjem, zpracování a interpretace vstupní informace.

Každý si určitě všiml, že jednotlivé vjemy vnímáme dost individuálně. Ukázali jsme si to na příkladu s barvami, no takto to funguje i pro všechny ostatní smysly. Každý vnímá trochu jinak teplo, zvuk, chutě, vůně nebo bolest. Dokázat to můžeme minimálně z fyzikálního hlediska, protože každý má jiný počet buněk s příslušnými receptory, trochu jiné prahy pro příjem signálů a také trochu jiné zpracování mozkem. No a každý z nás to taky trochu jinak interpretuje. Interpretace samotná je hodně důležitá, protože je ovlivněna naší pamětí, existujícími znalostmi, očekáváním, výchovou a prostředím či kulturou, ve kterých žijeme. Subjektivita ve vnímání tedy hraje velkou roli i mimo fyzikálně-chemické aspekty.

Ok, možná vnímáme okolitý svět malinko jinak. Když se ale podíváme například na stůl, shodneme se všichni, že vidíme stůl? Řekněme, že téměř jistě ano. Většina vnímaných věcí je více méně jasná a všichni tak nějak víme, co vidíme, co slyšíme, o čem se mluví a tak dále. Existují ale určité skutečnosti, které až tak moc jasné nejsou. Nejde jenom o skutečnosti typu odstínu barvy, vnímání chutí nebo jiného pocitu teploty. Ve světě existují i takové věci nebo jevy, které vnímáme naprosto zkresleně. Mezi nejznámější takové "vyhodnocovací chyby" patří optické klamy neboli iluze. Podívejme se na následující tři obrázky, které znázorňují takovéto klamy a které pravděpodobně i znáte.

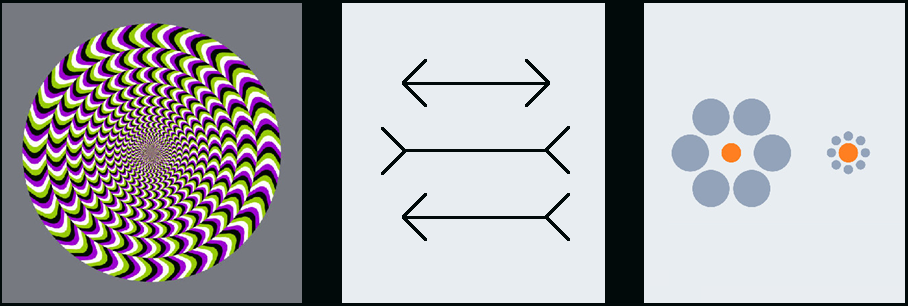
Obrázek vlevo v nás vyvolává dojem, že se ten kruh (nebo jeho části) otáčejí. Když se ale přiblížíme, tento dojem mizí. Celá iluze je způsobena uspořádáním barev a vzdáleností našich očí od obrázku. Dále tam vidíme tři šipky a máme pocit, že jejich úsečky jsou různě dlouhé. V tomto případě je klam vyvolaný samotnými šipkami přidanými k úsečkám. Různě "větvené" linky nám tedy zkreslují jejich skutečnou velikost. No a na obrázku vpravo se zdá, že oranžové kruhy jsou různě velké. Jenomže ony jsou stejné a klam je vyvolán tím, že velikost předmětů naše mysl určuje tak, že je porovnává s objekty v okolí. Takže oranžový kruh vlevo se zdá menší, protože v jeho okolí jsou větší kruhy, zatímco oranžový kruh vpravo se zdá větší, protože v jeho okolí jsou kruhy menší. Proto se nám třeba i Slunce těsně nad horizontem jeví jako větší, než když je uprostřed dne vysoko na obloze, kde v jeho okolí nic není.

Iluze se netýkají jenom vidění, ale všech našich smyslů. Ke zkreslením často dochází například i u zvuku. Určitě znáte takové ty vtípky, jak vám někdo pustí zvuk a vy máte uhodnout, co ho vyvolává. Třeba kočičí křik připomínající pláč dítěte. Tady si všimněte, že u sluchu nám často chybí ujištění zrakem. Nebo existují určité finty při saunování - vhodné proudění horkého vzduchu může na vaši kůži vyvolat mrazivý pocit, i když je uvnitř sauny neskutečně horko. Nesprávná interpretace různých skutečností se ale netýká jenom smyslů. Vzpomeňte si, jak jsme v prvním článku o pravdě mluvili o kouzelníkovi. Ten dokáže vyvolat takové iluze, které mohou ošálit i náš zdravý rozum a nemáme vůbec páru, jak daný trik provedl. Interpretace reality je tedy velmi záludná. A to neberu do úvahy různé kognitivní disonance a konfirmační zkreslení v rámci psychologických jevů. Ty jsou ještě víc komplexnější, protože jsou do toho zapojeny i naše emoce a vnitřní prožitky.

Ke slovu se tak hlásí matematika, protože ona nám může hodně pomoct ty iluze odhalit. Ona totiž nespoléhá na smysly a na to, čemu věříme. Spoléhá pouze na myšlenkové procesy a abstrakce. Zkusme se například podívat na následující obrázek.

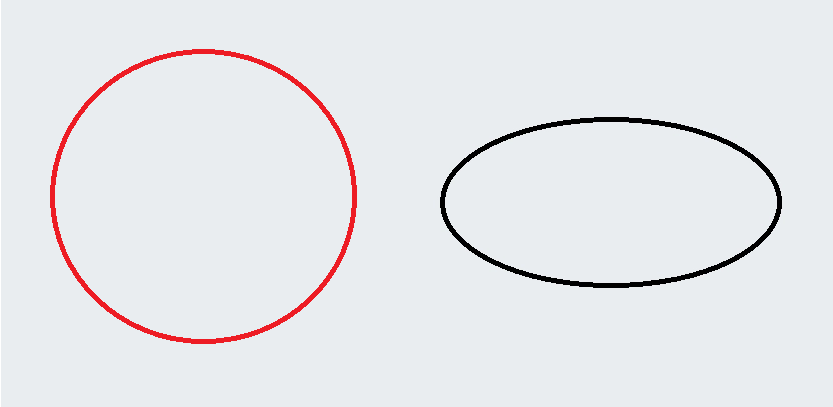
Vidíme dva objekty - kruh a elipsu. Na tom se asi shodneme, takže není tu nic subjektivního. Určitě jste si ale někdy taky všimli, že když se na kruh díváte ne shora, ale víc zboku, tak se jeví jako elipsa. Nebo když svítíte baterkou na nějakou kouli zešikma, tak taky vrhá stín ve tvaru elipsy. Nejsou tedy kruh a elipsa jenom dva různé projevy té samé věci? Ano, jsou. A můžeme to dokázat pomocí celkem snadné geometrie, která je znázorněna na dalším obrázku.

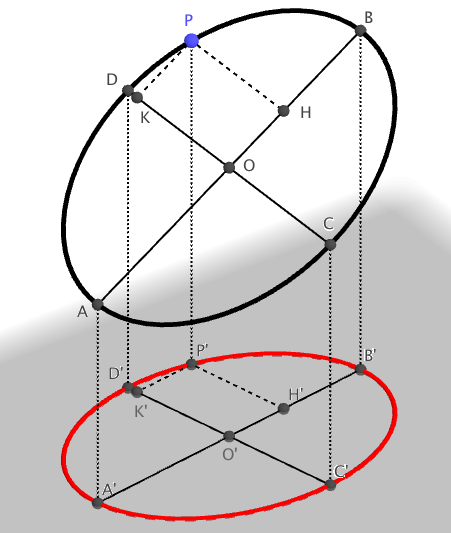
Z obrázku je patrné, že pro každý bod na elipse existuje přesně odpovídající bod na kružnici. Ono to platí i pro jakýkoliv bod, kdyby se jednalo o celou plochu nebo i objem v případě tří rozměrů. Kruh a elipsa je ta samá věc, jen viděna z jiné perspektivy. Klame nás v tom náš samotný zrak! Ono nejenom kruh a elipsa jsou určité perspektivy jedné a té samé věci. Taky sem patří hyperbola a parabola. Všechny jsou určitým vyjádřením stejného matematického objektu, ale především náš zrak nás nutí to vidět jako různé věci. Koho by to zajímalo víc, může si vygooglit něco o kuželosečkách.

Někdo by ale mohl namítnout: "No, ale když si vezmu nějakou ohebnou obruč, můžu z ní přece udělat elipsu. Nebo naopak, z elipsy pak udělat zpětně kruh. A to už není jenom perspektiva!"
Problém této námitky spočívá v terminologii. Konkrétně se tu nehodí slovo "perspektiva", protože její význam je spojen především s tím viděním, což nám kazí celou pointu. Daleko lepší je zvolit slovo reprezentace. Je to něco podobného, jako když si vezmete váleček plastelíny a můžete z něho udělat kouli, krychli nebo i slona, jestli chcete. Všechny vymodelované objekty budou jenom jakousi reprezentací jediné a té samé plastelíny. Nebo jako druhý příklad můžeme uvést sportovní reprezentaci. Třeba na mistrovstvích světa ve fotbale se scházejí reprezentační týmy různých zemí, no všechny prezentují to samé - fotbal.

Když tento princip aplikujeme i na matematiku, tak zjistíme, že například radioaktivní rozpad, nabíjení akumulátoru, bakteriální růst nebo složené úročení vykazují tou samou závislost, kterou můžeme reprezentovat třeba prostřednictvím grafu. Všechny tyto jevy se chovají podle stejné zákonitosti. Jenže pozor, graf je jenom vizuální reprezentace pro lepší představu, ale samotná závislost je přírodní jev, který odhalila naše abstraktní mysl a ne smysly. Protože i kdyby byl někdo hluchý a slepý, stále má svou mysl, která je schopná si představit cokoliv a následně to vyťukat třeba morseovkou do našeho ramena.

Začínáte už aspoň trochu vnímat to kouzlo matematiky? Ona je totiž schopná konstruovat právě různé takové reprezentace (anebo i projekce) jedné a té samé věci, a dokáže tak vidět souvislosti i tam, kde je naše smysly vůbec nezachytí. To naše mysl je zachycuje. Třeba díky různým projekcím dokážeme bez problémů popsat dimenze se sto rozměry, no naše schopnost vizualizace si s tím ani neškrtne. Matematika tedy není nic jiného než vysoký stupeň abstraktního myšlení, a proto je vhodné výrok Galilea trochu poopravit: Chápat přírodu a svět totiž nemusí jen ten, kdo ovládá kalkul, ale kdokoliv, kdo disponuje abstraktním myšlením a vidí ve věcech i to, co naše smysly nezachycují nebo dokáže odhalit zmíněna smyslová zkreslení. Kdyby se většina takových lidí o matematiku začala zajímat, pravděpodobně by s ní neměla vůbec problém a rychle by ji pochopila. Třeba je známé, že malíři, kteří kreslí obrazy s vyjádřením hloubky a perspektivy, jsou v podstatě excelentní geometři.

Vraťme se ale ještě na chvíli k naším smyslům a trochu si zaspekulujme, jestli různá zkreslení či iluze jsou opravdu to jediné, co mate naše smysly.
Málokoho napadne, že v průběhu percepce může existovat i možnost vzniku chyby. Všichni jsou si tak nějak jistí, že vidí, slyší nebo nasávají vůně naprosto bezchybně. Když si ale uvědomíme, kolika buňkami a nervovými dráhami vstupní signál prochází, existuje určitá šance, že se někde něco "porouchá" nebo "zpřehází". Nemusí jít nutně o nějaké poruchy nebo nemoci, ale některé signály se můžou přenášet s nějakou chybovou odchylkou a my pak celý život vnímáme nějaké vjemy trochu jinak než jiní lidé. Navíc, existují i tací lidé, kteří mají tu odchylku výraznou. Například, vyskytuje se poměrně velká variabilita ve vnímání bolesti. To je docela viditelné u žen při porodech. Některé nevydají téměř ani hlásek a jiné z té bolesti téměř umřou. Vzácně se vyskytne i takový případ, kdy dotyčný necítí bolest vůbec. Nejde ale jenom o bolest. Někteří jsou schopni vnímat vyšší frekvence zvuku či mají silně vyvinutý čich. Je tohle všechno ale skutečně odchylka? Není náhodou variabilita vnímání prostřednictvím smyslů spíš přirozená, abychom si mohli vzájemně sdělovat rozmanitost reality? Podívejme se dál.

Všichni tak nějak považujeme za naprosto zřejmé, že lidé vnímají jednotlivé smysly odděleně. Ale co když ne? Existuje totiž relativně častý jev zvaný synestezie, při kterém člověk prožívá vjemy propojeně. Třeba při pohledu na číslice vnímá barvy. Já jednoho takového člověka znám a když mu napíšete na papír například dvojku, automaticky ji vidí modře. Jiní lidé zase často vnímají barvy při slyšení čistých tónů a když poslouchají hudbu, doslova "vidí" barevnou symfonii. Existují ale i mnohem divočejší propojení. Například, při vyslovení slova auto někdo cítí v ústech chuť banánu. Nebo když někdo jí chleba, cítí dotykové vjemy - třeba lechtání na kůži. Nebo při vyslovení jmen někdo vnímá prostor (Petrové sú vlevo, Hanky více vzadu než Lenky). Jiní při pohledu na lidi vidí aury (taky jednoho takového člověka znám). Mimochodem, já sama vnímám při určitých slovech lokální projevy tepla a navíc, i v konkrétních částech těla. Některá slova jsou prostě "teplejší" než jiná. Takže pokud někdo z vás prožívá zvláštní vjemy, vůbec si z toho nic nedělejte!
Je toho tedy opravdu dost a ještě jednou připomínám, že synestezie jsou mezi lidmi relativně časté - přinejmenším 10 % populace. O dalších se neví, protože lidé se o "podivnostech" bojí mluvit. Navíc, "nositel" synestezie to vůbec nevnímá jako něco divného. Pro něj to je běžná součást života.

Co způsobuje tato propojení vjemů, není zatím detailně prozkoumáno, ale neřadí se to mezi poruchy. Tento podivný "dar" lze považovat za něco podobného, jako je například i leváctví a vyskytuje se zhruba šestkrát častěji u žen. Existuje také teorie, že všechny malinké děti mají smysly mnohem víc propojené a jak se následně vyvíjejí, tak se jednotlivé smysly "odpojují". Zajímavé také je, že podle historických údajů určitými synesteziemi "trpěli" například i E. A. Poe, Baudelaire, Beethoven, Schubert či van Gogh a v podstatě díky tomu byla jejich díla unikátní, protože vnímali svět víc "propojeně".

Další věc, kterou musíme brát v úvahu, je jakási "vzdálenost" mezi námi a objekty, které vnímáme. Když se třeba koukáme na stůl, jeho obraz nám vytvářejí fotony světla z něho odrazené a které dopadají na naši sítnici. Jenomže ty fotony nejdříve letí vzduchem, pak procházejí okem, následně interagují s buňkami sítnice, tam dojde k určitým molekulárním změnám a ty změny vyvolají nervový vzruch. No a ten vzruch pak ještě musí urazit další vzdálenost, kým docestuje do příjmové oblasti mozkové kůry. To je docela komplexní proces. Navíc, dle kvantové mechaniky jakákoliv mikroskopická interakce mění skutečný stav interagujících objektů. Nebo jinými slovy, mikroskopickou interakcí se původní informace ničí. A týká se to všeho - našich těl i jakýchkoliv měřících přístrojů. Takže náš mozek vždycky registruje jenom jakési neúplné a pozměněné informace přicházející ze smyslů. Schrödinger o tomhle problému řekl, že my v podstatě "zabíjíme" skutečnost a vnímáme mrtvou realitu.

Když se nad tím vším zamyslíme, zdá se, že příčinou neúplnosti vjemů je jakási "vzdálenost" mezi pozorovatelem a pozorovaným objektem (subjekt versus objekt). Ta vzdálenost nemusí být nutně "prostorová", mám spíš na mysli nutnost výměny informací, čímž vzniká určitá dekoherence. Potom je samozřejmě i těžké určit, co z toho je vlastně pravdivé a co falešné. Jenomže ta pravdivá skutečnost tady někde určitě je a kdyby mezi subjekty a objekty existovala bezprostřednost (žádná "vzdálenost"), pravděpodobně bychom vnímali pravdivější realitu. Ne nadarmo spirituální obory mluví o sjednocení. Oni vlastně mluví o tom samém!

A teď se zkuste zamyslet ještě víc. Když se podíváte na svou ruku, jistě je mezi ní a vaším subjektivním vjemem jakási ta "vzdálenost". Položím tedy jednu provokativní otázku: Je vůbec vaše tělo pravdivé? Jste si tím naprosto jistí? Je to přece jenom vaší myslí vnímaný objekt. Existence našich těl je spíš jistota morální než fyzická! Když se vás ještě zeptám: Co ve vaši existenci vnímáte naprosto bezprostředně? Není to náhodou pocit vašeho já? Pocit vašich myšlenek? S nadsázkou bychom mohli říct, že naše já a naše vědomí jsou pravdivé, protože si uvědomujeme sami sebe - subjekt a objekt jsou jedno, není tam žádná "vzdálenost", žádná dekoherence. No, ale nebudeme zbytečně věci komplikovat a filozofování tady raději stopneme.

K smyslům na závěr jenom tolik, že musíme být opravdu opatrní, pokud něco vidíme, slyšíme nebo cítíme a chceme to sdělit i ostatním. Nepřesvědčujte je, že tohle triko je smaragdově zelené, tohle jídlo moc pálivé, že slyšíte pískání nebo že je dnes šílená zima. Oni to s velkou pravděpodobností stejně vnímají trochu jinak...


Emoce

Emoce jsou náročná záležitost, při které se zastavíme jenom na chvilku, protože tenhle jazyk přírody zatím není hlouběji objasněn. Náš emoční stav závisí jednak od našich myšlenek, druhak od zevního prostředí a smyslových vjemů. To pak způsobuje konkrétní stav našeho rozpoložení - jsme šťastní, smutní, rozčílení, pokojní, překvapení, bojíme se a tak dále. S emocemi je to složité i z dalšího důvodu - některé jsou "nižší" a vyskytují se i u zvířat, například strach, radost, úzkost anebo i láska, a pak jsou tady emoce "vyšší", které jsou typické pro lidi a vyžadují už komplexnější vědomí. Patří sem například pocit výčitek, pýcha, existenciální úzkost, nostalgie anebo ironické a sarkastické prožívání.

Vzniklé emoce pak působí formou zpětné vazby znovu na naše myšlení a chování a nad tím se musíme trochu zamyslet, protože takové "smyčky" mohou být příčinou patologického vzorce v našem vnímání. Je to viditelné například u neurotických potíží, kdy se člověk cyklí v těch samých emocích a postojích. Člověk je potom vlastně úzkostnější z úzkostí a depresivnější z depresí. 
Je tedy dobré se vlastními emocemi zabývat a vypozorovat, jak se vlastně projevují a jestli v dané chvíli jsou vůbec nějak významné nebo přínosné. Emoce ovlivňují naši mysl výrazně, což má určitě dopad i na samotné hledání pravdy. Přílišný strach, rozčílení nebo vzrušení správnost našeho uvažování spíš ohrožují, a proto je žádoucí, aby byl člověk při hloubavém dumání poněkud "klidnější".

Matematika a síla abstraktního myšlení

Teď si ukážeme pár příkladů, kde čistě abstraktní myšlenkové postupy dokážou vyplodit naprosto kontraintuitivní nebo podle někoho i nemožné závěry. Ale přesto jsou tyto závěry správné, protože celý postup jejich odvození je striktně logický.

1. Různě velká nekonečna
Představte si, že máte přirozená čísla - 1, 2, 3, 4, 5 a tak dále až do nekonečna. Co si myslíte, kolik je sudých čísel? Intuitivně bychom řekli, že asi teda dvakrát míň. Jenomže pravda je taková, že sudých čísel je stejně mnoho jako přirozených. Důkaz je jednoduchý a spočívá v "párování". Uděláme to tak, že každému přirozenému číslu přiřadíme číslo sudé a vytvoříme tak páry, tj. 1 → 2, 2 → 4, 3 → 6, 4 → 8 a tak dále. No a kdybychom takhle pokračovali do nekonečna, vždy by byla k dispozici čísla pro spárování. Z toho vyplývá, že jak přirozených čísel, tak sudých čísel je stejně mnoho a jejich nekonečna jsou tedy stejně velká. Nemusíme ani nijak dál dokazovat, že to platí i pro čísla lichá.
Když si ale vezmeme desetinná čísla, zjistíme, že při párování nám vždycky nějaké zbyde navíc. Nekonečno desetinných čísel je tedy větší než nekonečno přirozených nebo sudých čísel. Důkaz už je náročnější, tak ho nebudu uvádět. Ono dokonce i mezi pouhou nulkou a jedničkou je desetinných čísel víc než všech přirozených. Takže nekonečno desetinných čísel je extrémně větší než nekonečno přirozených čísel! A to ještě jenom začínáme. 🙂

2. Narozeniny
Představte si, že náhodně vyberete pár lidí a zeptáte se jich, který den v roku mají narozeniny. Víte, kolik lidí vám stačí na to, aby alespoň dva z nich měli víc než padesátiprocentní šanci, že mají narozeniny ve stejný den? Stačí vám na to 23 náhodně vybraných lidí. To je docela málo! Pravděpodobnosti jsou záludné, takže se podívejme na další příklad.

3. Hrajeme tenis
Mějme talentovaného kluka v tenise. Představme si, že bude hrát klasický zápas na tři sety se svým otcem a s profesionálním tenistou. Každý set bude hrát na střídačku jednou s otcem a jednou s profesionálem a chceme, aby kluk vyhrál dva sety za sebou. Máme tedy dvě možnosti pořadí: otec/profesionál/otec, nebo profesionál/otec/profesionál. Co myslíte, která varianta je výhodnější, aby kluk vyhrál dva sety za sebou? Většina lidí intuitivně řekne: "To je přece jasné, otec/profesionál/otec! Vždyť tam bude jenom jeden set s profesionálem, takže kluk bude ve větší psychické pohodě!" Věřte ale, že větší šanci na výhru má kluk tehdy, pokud si vybere druhou možnost. Pravděpodobnosti jsou záludné...

4. Pásek kolem Země
Představte si, že natáhneme dlouhatánský pásek kolem rovníku Země tak, aby pevně obepínal její obvod. Pak tento pásek přestřihneme a k oběma jeho koncům přišijeme další dva metry pásku a znovu ho napneme kolem rovníku. Co myslíte, o kolik se pásek nadzvedne nad povrch Země? Naše intuice nám řekne: "Vždyť jsme ho prodloužili jenom o dva metry. To se zvedne sotva o milimetr!" No pravda je taková, že se zvedne o tolik, že bychom ten pásek dokázali podlézt! Konkrétně se nadzvedne zhruba o 32 centimetrů. Zkuste si to vypočítat, stačí vám na to znalost obvodu Země.

5. Banach - Tarského paradox
Tenhle příklad je můj nejoblíbenější, protože zcela ničí lidskou intuici! Představte si, že máte kouli o průměru třeba jeden metr. Pokud tuto kouli rozkrájíte určitým, ale přesně stanoveným postupem na minimálně pět kousků, můžete je následně pospojovat tak, že dostanete dvě kompletní koule znovu o průměru jeden metr. A nikde nezbyde ani dírka. No sakra! Vždyť jsme udělali kopii koule z ničeho! Když je možné tohle, nemám vůbec žádné předsudky, když někdo řekne, že vidí ducha nebo UFO!
Chcete slyšet něco ještě praštěnějšího? Matematika, která stojí za tímto paradoxem, dovoluje udělat z citrónu objekt o velikosti Slunce! 👀 Že nemožné? No, zdá se vám to proto, že vaše smysly vás klamou v tom, jak vnímáte objem. Podle vašich přesvědčení totiž není možné zvětšit objem z "ničeho". No na základě jednoho axiomu platí, že když nějaký objekt rozdělíte na kousky, a poté ty kousky všelijak přeskupujete, objem se nezachovává. A víte, co je to za axiom, který tohle povoluje? On je vlastně velmi jednoduchý - axiom tvrdí, že existuje volba neboli výběr. A to přece poznáte i ze života - když si kupujete nové boty, taky máte na výběr. Na tom není nic abnormálního. No a tady se jen vybírá z matematických objektů. Taky na tom není nic abnormálního... Navíc, řešení je striktně logické, kdežto boty někdy vyberete i blbě. Tak co, věříte už na duchy?
(Mimochodem, tady mě napadlo, že pokud se nemusí zachovávat objem a my žijeme v časoprostoru, který nějaký objem jistě má, neplatí tedy náhodou i to, že se nemusí nutně zachovávat taky prostor a čas? 🤔)

6. Je Země placatá?
Tenhle příklad není žádný paradox, ale jelikož jsem zaslechla, že hodně lidí věří tomu, že Země je plochá, tak si v pár řádcích ukážeme, že tomu tak není. A znovu nám k tomu postačí znalost obvodu kruhu. Víme, že poměr obvodu kruhu a jeho průměru se rovná slavnému číslu π. Tohle platí pro placatý kruh. Pojďme si to i ověřit. Pokud máme průměr kruhu například tři metry, jeho obvod bude po zaokrouhlení přibližně 9,424778 m. Když si pak dáme do poměru tento obvod a průměr kruhu, bude se to logicky rovnat přesně π. Na prvních pár desetinných čísel je π rovno 3,141592. Nic zajímavého. Prostě kruh.
A teď pointa - tohle neplatí pro kouli. Jednoduše, poměr rovníkového obvodu koule a jejího průměru se nerovná π. Může za to zakřivení její plochy a třetí rozměr. Pojďme se tedy podívat na Schrödingerovou Zemi. Její rovníkový obvod se rovná 40 075 kilometrů a její průměr je 12 756 kilometrů. Pro jistotu si to plochozemci můžou na té údajné placce i změřit - nejdříve obejít celý rovník a pak jít furt rovně na druhou stranu. Tak, a teď si to dejme do poměru, jestli se to bude rovnat π. No, nebude. Výsledek je 3,141659. Ups...
Jistě, plochozemci by mohli namítnout, že je to dáno nějakou nepřesností nebo nedokonalostí té podezřelé koule, ale můžu je ujistit, že i kdyby byla Země dokonalá koule, tento poměr bude prostě jiný než přesné pí. Toto mystické číslo totiž vyplývá z rovinné geometrie, tedy z kruhu na papíru. Pokud vím, my ale žijeme v jaksi "jiném" geometrickém uspořádání. Člověk by nevěřil, že matematika dokáže odhalit i dezinformace.


Neúplnost jazyků

Dobře. Matika je super a je jednoznačně jazykem tvorby. Když se podíváme na dnešní moderní svět, z obrovské části je založen právě na matematice - technologie, digitalizace, algoritmy, ekonomie, věda... Za tohle všechno skutečně vděčíme matematice! Bez jejího aplikování bychom stále žili někde v pralese, takže až někdy narazíte na podivně vypadajícího šprta, poplácejte ho po rameni a projevte mu trochu úcty.
Je ale matematika skutečně tak dokonalá? Bohužel, ani ona nedokáže vysvětlit pravdu vesmíru. Minimálně ne v současné podobě. Už v prvním článku o Pravdě jsme zmínili Alfreda Tarského, který dokázal, že jakýkoliv jazyk je neúplný a neumí popsat sám sebe. Byť je sebevíc konzistentní a logický. Potřebujeme na to něco "víc", něco, co pochází z oblasti za hranicemi tohoto jazyka. Platí to i pro matematiku a logiku. Naše mysl tedy musí najít nějaký další jazyk, který bude schopný řešit současné logické neúplnosti a nejednoznačnosti. Bude to něco jako "Myšlení 2.0".

Do problému této neúplnosti se nadšeně pustil brilantní matematik a logik Kurt Gödel a dospěl k zajímavému zjištění. Možná jste o tomhle chlápkovi ještě neslyšeli, tak vám o něm i něco málo povím. Gödel byl v posledním desetiletí Einsteinova života jeho nejbližším přítelem. Ten si Gödela neskutečně vážil, protože Einstein sám nebyl v matematice nějak významně excelentní. On sice měl silnou intuici, jak ten časoprostor vypadá a viděl ho ve své hlavě, ale aby svou teorii relativity napsal odborným jazykem, musel se matematiku poctivě doučit od těch nejlepších tehdejší doby. Einstein prý lidem vyprávěl, že je pro něj ctí doprovázet Gödela každý den cestou do práce. Godël byl velkým obdivovatelem Leibnize a ačkoliv byl logikem těžkého kalibru, zastával se metafyziky a byl hluboce věřící člověk (ne ve smyslu "oficiální" církve). Někteří ho dokonce nazývali druhým Aristotelem. Jo a jméno Gödel se úzce pojí s Tarskim a Turingem - oni všichni položili základy pro dnešní počítače.

No a na co tedy tenhle chlápek přišel? Přišel na mnoho věcí, ale pro tento článek jsou důležité jeho dvě věty o neúplnosti, které navazují na práci Tarského. Snažit se je nějak srozumitelně popsat nebo znázornit je extrémně náročné, takže si povíme jenom jejich pointu.
Pokud se v přísně logickém uvažování vyskytne nejednoznačnost, automaticky se bere za nepřijatelnou. Jednoduše, nejednoznačnost nemá při hledání pravdy co dělat. Neschopnost "rozhodnout se" je v logice přesně to samé, co představují klamy a iluze ve smyslovém vnímání! Je to jakési "zatemnění" našich myslí. Gödel ale kápnul božskou - přišel na to, jak "obejít" tyto nejednoznačnosti neboli spory, paradoxy. Gödel ukázal, že jakmile se v nějakém jazyce vyskytne spor, tenhle jazyk se při hledání jednoznačné pravdivosti stává passé... A právě tady musíme rozbít staré dogma - musí nutně při hledání pravdy platit bezespornost? Gödel dokázal, že nemusí a že spory nám paradoxně mohou pomoct i pravdu odhalit. Právě na jejich základě totiž vznikly tyto věty o neúplnosti, které pravdivé jsou.
Takže, jakmile se v daném jazyce vyskytne spor, pro který nelze zkonstruovat důkaz, tak v tomhle jazyku tenhle spor nevyřešíme. Potřebujeme jazyk jiný. Gödel taky ukázal, že dokonce existují i také pravdy, které stejně nikdy nedokážeme. A to už je i filozofický problém, protože to značí, že naše současná mysl nikdy nedosáhne veškerého poznání. Takže buďte v klidu, když si vaše dnešní já neumí něco vysvětlit. Je to normální...

Co z toho všeho vyplývá? Že problémem nejsou samotné spory nebo paradoxy, ale naše neschopnost řešit nejednoznačnost, pokud na ni narazíme. Vzpomeňte si na paradox lháře. Jednoduše, naše mysl zatím postrádá postupy, jak dokázat něco sporného, i když to třeba pravdivé skutečně je. Naše mysl je totiž nastavená tak, že předpokládá a očekává bezespornost. Gödelovy důkazy nám taky říkají, že pokud je daný jazyk postaven na předpokladech, bude vždy neúplný. A týká se to i samotné matematiky. Byť je to to nejpravdivější, co zatím máme. Ani ona není úplná a naráží na spory, kterých pravdivost neumí dokázat. Musíme si tedy skutečně počkat na Myšlení 2.0 a nalézt nové jazyky, které nám při hledání pravdy pomůžou zase trochu víc. Jaký jazyk to bude, to nevíme. Ale určitě si bude vyžadovat větší uvědomění.

Mimochodem, Gödelovy věty mají velký vliv i na to, čemu dnes říkáme umělá inteligence. Ta je algoritmická a je založena na čisté matematice, takže vězte, že ani AI nevyřeší všechno. Každý jazykový model a algoritmus má své limity, protože vychází z předpokladů. A předpoklad znamená neúplnost. A taky problémů k řešení je daleko víc než počet všech možných algoritmů...


Intuice

Intuice je tak jako matematika docela zvláštní. Říká se ji i šestý smysl a všichni ji tak nějak "intuitivně" chápeme. Ale co to vlastně je a jak ovlivňuje naše životy, to neví nikdo. O intuici se vedou rozsáhlé filozofické debaty, které její pochopení spíš komplikují, než aby ji objasnily. Intuice je tedy rozhodně těžce vysvětlitelný pojem. Je to to samé jako pochopení kauzality, o které jsme se bavili v minulém článku. Všichni tak nějak intuitivně víme, co slovo příčina znamená, ale dokázat příčinnost nějakého jevu může být extrémně těžké.

Určitě jste již všichni zažili ten vnitřní pocit, který k vám telepaticky promlouval: "Tohle udělej! ... Tam nechoď! ... Ano, tohle je pravda!" a vám se to potom nějak vyplatilo. Jenomže ono se někdy i stává, že intuice zklame a vám se to nevyplatí. Z čeho tedy pramení takový ten pocit jistoty, který nemusí být nutně správný?
V první řadě si musíme uvědomit, že intuice je dynamická a vyvíjí se. Vaše intuitivní schopnosti určitě byly na jiné úrovni před dvaceti lety, než je vnímáte dnes. Jsou ovlivněny minimálně našimi zkušenostmi a pamětí, no a taky se u lidí liší. Obecně ale lze říct, že intuici více využívají lidé, kteří jsou zkušenější, empatičtější, kreativnější, otevřenější, spontánnější a dále ti, kteří mají vyšší míru sebereflexe. Též lze vypozorovat, že intuitivnější jsou ženy (vlastně být i musí, protože jinak by nevycítili, co vlastně mají dělat s miminkem, když se narodí).

Kam ale intuice vlastně spadá? Dalo by se říct, že leží někde mezi našimi smysly, vnitřním světem a našim rozumem. Za prvé, schopnost intuice hodně závisí na pozorování, ale má širší záběr sahající mnohem dál než naše smysly. Záleží tedy na našich zkušenostech, které v životě získáváme. Například, mladý lékař, který je krátce po škole, má daleko větší potíže s odhadem stavu pacienta než starý zkušený lékař. Ten zkušený dokáže pacienta prokouknut už při vstupu do ordinace, protože má vypozorováno mnoho detailů - chůzi pacienta, jeho barvu kůže, dech, stav vědomí, emoční rozpoložení a tak dále. Jednoduše, ten zkušený lékař už toho hodně viděl, slyšel a navnímal z každodenního kontaktu s nemocnými lidmi. No ten mladý lékař zatím tohle všechno postrádá, takže se opírá především o své znalosti získané ve škole a taková ta "plynulost" v rozhodování mu zatím chybí a jeho intuice postupně sílí, jak získává zkušenosti. Máme tedy jakousi intuici "nováčka" a intuici "experta", která závisí od pozorování a našich smyslů. A tak to v našich životech platí i pro všechno ostatní, co si vyžaduje zkušenosti.

Na druhé straně, schopnost intuice je taky silně ovlivněna naší schopností logicky myslet, což nezávisí až tak moc na věku a zkušenostech. Když vám předložím tvrzení, že pokud a < b a b < c, pak i a < c, intuitivně se rychle zorientujete, oč tu kráčí. Když vám ale řeknu, že pokud a < 1, pak 2 - 2a > 0, už nad tím musíte trochu přemýšlet, protože to není na první pohled tak jasné. Intuice si tedy někdy vyžaduje i rozumového úsilí a pochopení daného jevu. Nalezení souvislostí totiž umožňuje rozumové intuici operovat s větší lehkostí a třeba nám to i pomůže vyřešit nějaký mnohem komplexnější problém. Dalo by se říct, že tento typ intuice je nepostrádatelný, pokud chcete excelovat v IQ testech nebo se chcete stát úspěšným obchodníkem či vojenským stratégem.

Když to tedy shrneme, intuice založena na našich smyslech a zkušenostech je reflexivní, rychlá, automatická, bez námahy, bez nějaké významné introspekce a závisí na čase a paměti. Ve světě, kde je primárním cílem přežití a hledání jednoduchého řešení, je tedy zkušenostní intuice daleko lepší.
No a naopak, rozumová intuice je pomalá, kontrolovaná, náročná, transparentní a je na čase nezávislá. Tento typ intuice je vhodnější při zkoumání detailů a komplexních souvislostí a je větší pravděpodobnost, že s touto intuicí i něco nového vymyslíme.

Zajímavé ale je, že některé intuitivní schopnosti nejsou ani smyslové, ani rozumové, ale vynořují se odněkud z neznáma. I mnoho slavných vědců o sobě říká (nebo říkalo), že jejich objevy nespočívaly v pečlivém uvažování, ale navedla je k nim jejich intuice. Nějak věděli, že zrovna tohle je pravda a až následně provedli podrobný rozbor, jestli to sedí i logicky. Paradoxně i ti nejslavnější matematici vyvinuli své teorie spíš intuitivně "shora", než aby je stavěli "odspodu". Nejdříve přišla ta intuice a až pak ty detailní kroky s důkazy.
Tento typ intuice se taky vyskytuje u špičkových šachistů. Bylo provedeno hodně studií, které se snažily zjistit, jak uvažuje takový šachový expert. No a ukázalo se, že ti popřední světoví mistři při hraní používají spíš intuici než promakanou strategii. Bylo provedeno i pár studií se zobrazením mozku a mistrům se více "rozsvítily" oblasti zaměřené na rychlou vizuálně-prostorovou orientaci a rozpoznávání objektů a těm průměrným spíš oblasti pomalého, strategického a aritmetického uvažování.

Jak tedy funguje intuice, to přesně neví nikdo. Ale její síla hodně záleží na celém našem bytostním komplexu - na smyslech, na rozumu, na zkušenostech a taky na emocích a vnitřním světě. Intuice je každopádně reálným jevem, a proto není od věci si někdy jen tak sednout a poslechnout si naše srdce, co nám chce říct. Může mít totiž pravdu.

Závěr

Co je vlastně Pravda?

Těžko říct... Vesmír nám na její hledání poskytuje různé jazyky - mluvenou řeč, formální logiku, matematiku, smysly, emoce, intuici... To všechno nám poskytuje nějaké informace, které jsou ale neúplné, protože v každé sféře našeho života narážíme na nejednoznačnosti. Ty nejednoznačnosti se pak snažíme řešit na základě nějakých předpokladů a předpoklad sám o sobě znamená, že vycházíme pouze ze skutečnosti, ale ne z jednoznačné a úplné pravdy. Ale to nevadí, naše mysl může mezi všemi těmi jazyky nalézat nové souvislosti, čímž ji zároveň pozdvihujeme na vyšší úroveň a třeba objevíme i jazyk jiný. A pokud si tyto souvislosti i navzájem sdělujeme jako bytosti, střípky reality se spojují a stávají se daleko jasnější...

No a kdybychom seděli u piva a zeptali jste se mě, co je pravda, víte, co bych vám odpověděla? Že pravda je vše, co si dokážete obhájit. Netvoříme si tedy pravdu sami? Ale bacha, někteří lidé si svou pravdu obhájí tak dobře, že jím věříte i celý život! Proč ale vlastně někomu nebo něčemu vůbec věříme? Ale o tom až příště...